Resit Assessment Model Answer
This is the model answer for the resit assessment.
In marking the assessment, partial marks are given for working, and for error carried forward (ECF), where an answer is correct but for an incorrect value brought forward from an earlier question for which the student has already lost marks.
A demo of the model answer code is available on Replit. The test code that was used in marking the assessments is available on GitHub
Part 1: Number Theory [ 30 marks ]
Numerical Systems [ 9 marks ]
- Use binary addition to find the result of \( 10001101 + 01101011 \)? Assume numbers are stored with 8 bits. You must show your working to get the mark. [ 1 mark ]
10001101 01101011 + -------- 11111000 - Use binary multiplication to find the result of \(10011 \times 1011 \)? You must show your working to get the mark. [ 1 mark ]
10011 1011 x -------- 10011 100110 0000000 10011000 + -------- 11010001 - Use binary division to find the remainder and quotient of \( 00111011 \div 00000011 \)? You must show your working to get the mark. [ 2 marks ]
___10011 11 |00111011 11 - ------- 1011 11 - ------- 101 11 -------- 10 quotient: 10011 remainder: 10 -
Implement the following methods in Java. You must not make use of built-in methods, such as
Integer.parseInt()to parse the Strings. You must not represent the binary values as numerical data types such asint. [ 3 marks ]/** * This function accepts one binary string (a String containing only the * characters '0' and '1') and returns the two's compliment of the binary * number. Represent the final number using the same number of bits as the * input string. * @param a - The binary number * @return A String representing the two's compliment of the argument. **/ static String twosCompliment(String a)
- Convert the decimal number 247 into hexadecimal. You must show your working to get the mark. [ 1 mark ]
- What is the base 16 number `abc` in decimal? You must show your working to get the mark. [ 1 mark ]
\( 247 \mod 16 = 7 = 7_{16} \)
\( \frac{247}{16} = 15 \)
\( 15 \mod 16 = 15 = f_{16} \)
\( \frac{15}{16} = 0 \)
\( 247 = f7_{16} \)
\( 10 \times 16^2 + 11 \times 16^1 + 12 \times 16^0 \)
\( = 2560 + 176 + 12 \)
\( = 2748_{10} \)
Modular Arithmetic [ 10 marks ]
- A binary relation R is reflexive and transitive. From this, which of the following must be true: [ 1 mark ]
- \( aRa \)
- \( aRb \)
- \( aRb \implies bRa \)
- \( aRb \wedge bRc \implies aRc \)
- \( aRa \) true
- \( aRb \) false
- \( aRb \implies bRa \) false
- \( aRb \wedge bRc \implies aRc \) true
-
Complete the following table of binary relations. Write
Tin a column if the relation has that property, orFif it does not. [ 2 marks ]Relation Reflexive Transitive Symmetric \( = \) T T T \( \equiv \) \( \subset \) \( \supseteq \) \( \iff \) \( \in \) \( \geq \) Relation Reflexive Transitive Symmetric \( = \) T T T \( \equiv \) T T T \( \subset \) F T F \( \supseteq \) T T F \( \iff \) T T T \( \in \) F F F \( \geq \) T T F
- You are working modulo 4. What is \( \frac{5}{3} \pmod{4} \)? Remember, your answer will be an integer. [ 2 mark ]
- Prove the following conjecture: If \( a \) even and \( b \) is odd, then \( a \times b \) is even.[ 1 mark ]
- Prove the following conjecture: \( 3(2n + 6)^2 +3 \) is not divisible by 2 [ 1 mark ]
- Prove the following conjecture by induction: The formula \( (2n + 5)(n + 5)(n + 3) \) is divisible by 3 for all positive natural numbers \( n \) [ 3 marks ]
\( \frac{5}{3} \equiv 5 \times 3^{-1} \pmod{4} \)
As \( 3 \times 3 \equiv 1 \pmod{4} \), \( 3^{-1} \equiv 3 \)
\( 5 \times 3 \pmod{4} \)
\( \equiv 15 \equiv 3 \pmod{4} \)
If \( a \) is even, then \( a = 2i \).
If \( b \) is odd, then \( b = 2j + 1 \).
\( a \times b = 2(i(2j + 1)) \). As this is divisible by 2 it is even. ∎
\( 2n + 6 = 2(n + 3) \) is even.
\( (2n + 6)^2 \) is even.
\( 3 \) is odd.
By our proof above, 3(2n + 6)^2 is therefore even, thus 3(2n + 6)^2 + 3 is odd. ∎
Base case \( n= 1\):
\( (2(1) + 5)((1) + 5)((1) + 3) \)
\( (7)(6)(4) = 168 = 3(56) \)
Case \( n = k\), we assume divisible by 3
\( 3 | (2(k) + 5)((k) + 5)((k) + 3) \)
\( 3 | 2k^3 + 21k^2 + 70k + 75 \)
Case \( n = k + 1\), we attempt to prove divisible by 3
\( 3 | (2k + 5)(k^2 + 10k + 24) \)
\( 3 | 2k^3 + 27k^2 + 118k + 168 \)
As we assumed above that \( 3 | 2k^3 + 21k^2 + 70k + 75 \)
\( 3 | (2k^3 + 27k^2 + 118k + 168) - (2k^3 + 21k^2 + 70k + 75) \)
\( 3 | 6k^2 + 48k + 93 \)
\( 3 | 3(3k^2 + 16k + 31) \) ∎
Algorithms [ 11 marks ]
- Simplify the following so that it is no longer uses sigma-notation: \( \sum_{i=1}^{n} (2i^2 + 5) \) [ 1 mark ]
\( \sum_{i=1}^{n} (2i^2 + 5) \)
\( = 2 \sum_{i=1}^{n} i^2 + \sum_{i=1}^{n} 5 \)
\( = 2(\frac{n(n+1)(2n+1)}{6}) + 5n \)
- Simplify the following so that it is no longer uses sigma-notation: \( \sum_{i=1}^{n} (i + \sum_{j=1}^{i} j) \) [ 2 marks ]
\( \sum_{i=1}^{n} (i + \sum_{j=1}^{i} j) \)
\( = \sum_{i=1}^{n} (i + \frac{i(i+1)}{2}) \)
\( = \sum_{i=1}^{n} \frac{i^2 + 3i}{2} \)
\( = \frac{1}{2} (\frac{n(n+1)(2n+1)}{6}) + \frac{3}{2} (\frac{n(n+1)}{2}) \)
\( = \frac{n(n+1)(2n+1)}{12} + \frac{3n(n+1)}{4} \)
- For each of the following, give their time complexity in Big-Oh notation. Then indicate which one is the slowest growing, and which is the fastest growing. [ 2 mark ]
- \( n^2 + 3n \)
- \( n! + \log n \)
- \( 3n \log n + 3n^2 \)
- \( e^n + n^3 \)
- \( 1 + 4\pi^3 \)
- \( 1 + 4\pi^3 = O(1)\)
- \( n^2 + 3n = O(n^2) \)
- \( 3n \log n + 3n^2 = O(n^2) \)
- \( e^n + n^3 = O(e^n)\)
- \( n! + \log n \) = O(n!)
- A function is defined as follows \( f(a, b) = \sum_{i=1}^{a} \sum_{j=1}^{(i + b)} j \).
- Give the value f(4,3) [ 1 mark ]
When \(i=1\), \( 1 + 2 + 3 + 4 \)
When \(i=2\), \( 1 + 2 + 3 + 4 + 5\)
When \(i=3\), \( 1 + 2 + 3 + 4 + 5 + 6\)
When \(i=4\), \( 1 + 2 + 3 + 4 + 5 + 6 + 7\)
\( f(4,3) = 4(1 + 2 + 3 + 4) + 3(5) + 2(6) + 7 \)
\( = 4 + 8 + 12 + 16 + 15 + 12 + 7 \)
\( = 74 \)
- Write a function named F in Java to implement this [ 2 marks ]
Here is the pseudo code for an algorithm
Function A(n)
num := 0
for (i = 1 to n)
for (j = 1 to i)
num := num + 1
endfor
endfor
return num
- Find the time function and express using summation [ 2 marks ]
- Give the time complexity of this time function [ 1 mark ]
\( c + \sum_{i=1}^n (c + \sum_{j=1}^i (c + c) ) \)
\( O(n^2) \)
Part 2: Discrete Mathematics [ 30 marks ]
Propositional Logic [ 9 marks ]
Assume shifts always shift in 0 and you are working with only 8 bits.
- What is
01010111 AND 11011011[ 1 mark ]01010011 - What is
LEFT SHIFT 00000101? [ 1 mark ]00001010 - You have two numbers with bits
10101010and00000001. Which combination of three or fewer bitwise operators can you use to get01010111[ 1 mark ]RIGHT SHIFT 10101010 = 01010101LEFT SHIFT 00000001 = 0000001001010101 OR 00000010 = 01010111RIGHT SHIFT 10101010 OR LEFT SHIFT 00000001
The First Distributive Law of Propositional Logic states that \( P \vee (Q \wedge R) \iff (P \vee Q) \wedge (P \vee R) \)
- Prove this law by means of a truth table.[ 3 marks ]
| \( P\) | \(Q \) | \(R \) | \( Q \wedge R \) | \( P \vee (Q \wedge R) \) | \( P \vee Q \) | \( P \vee R \) | \( (P \vee Q) \wedge (P \vee R) \) | \( P \vee (Q \wedge R) \iff (P \vee Q) \wedge (P \vee R) \) |
|---|---|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T | T | T |
| T | T | F | F | T | T | T | T | T |
| T | F | T | F | T | T | T | T | T |
| T | F | F | F | T | T | T | T | T |
| F | T | T | T | T | T | T | T | T |
| F | T | F | F | F | T | F | F | T |
| F | F | T | F | F | F | T | F | T |
| F | F | F | F | F | F | F | F | T |
Read the following example sentences:
- “If I am cold and I am wearing socks, then either it is not the case that my heating is working or I am ill.”
- “I am cold if and only if any of the following are true: I am not wearing socks, or I am ill, or it is not the case that my heating is working.”
- Identify the atomic propositions in these two sentences and assign each a letters (c = "I am cold", etc). [ 1 mark ]
- Using these letters as terms, express each example as a statement of propositional logic, using propositional logic symbols. [ 2 mark ]
C = “I am cold”
S = “I am wearing socks”
H = “my heating is working”
I = “I am ill”
Sentence 1: \( C \wedge S \implies \neg H \vee I \)
Sentence 2: \( C \iff \neg S \vee I \vee \neg H \)
Set Theory [ 14 marks ]
Assume the domain is the positive natural numbers (excluding 0). Given the sets
\( A = \{ 2, 3, 5, 7 \}\)
\( B = \{ n | n \mod 2 = 0 \}\)
\( C = \{ n | n > 5 \}\)
\( D = \{ n | n \equiv 2 \pmod{3}\}\)
\( E = \{ n | n \leq 10 \} \)
\( F = \{ 5, 6, 7 \} \)
- Describe in words the contents of the set \( B \) [ 1 mark ]
Even numbers
Give the extensions of the following sets:
- \( A \setminus B \) [ 1 mark ]
- \( A \cap C^C \) [ 1 mark ]
- \(\mathbb{P}(F) \) [ 2 mark ]
- \(F \times F \) [ 2 mark ]
\( \{ 3, 5, 7 \} \)
\( \{ 2, 3, 5 \} \)
\( \{ \emptyset, \{ 5 \}, \{ 6 \}, \{ 7 \}, \{ 5, 6 \}, \{ 6, 7 \}, \{ 5, 7 \}, \{ 5, 6, 7 \} \} \)
\( \{ (5, 5), (5, 6), (5, 7), (6,5), (6,6), (6,7), (7, 5), (7, 6), (7,7) \} \)
Give an intensional definition (using set builder notation) of the following sets:
- \( F \) (Do this without making reference to the set itself, i.e. not something like "\( x \in F \))"[ 2 marks ]
- \( \{ (1, 1), (2, 1), (2, 2), (3, 1), (3, 2), (3, 3) \} \) [ 2 marks ]
- \( \{ \emptyset, \{ 3 \}, \{ 4 \}, \{ 5 \}, \{ 3, 4 \}, \{ 4, 5 \}, \{ 3, 5 \}, \{ 3, 4, 5 \}, \) \( \{1\}, \{ 1, 3 \}, \{ 1, 4 \}, \{ 1, 5 \}, \{ 1, 3, 4 \}, \{ 1, 4, 5, \}, \{ 1, 3, 5 \}, \{ 1, 3, 4, 5 \}, \) \( \{2\}, \{ 2, 3 \}, \{ 2, 4 \}, \{ 2, 5 \}, \{ 2, 3, 4 \}, \{ 2, 4, 5 \}, \{ 2, 3, 5 \}, \{ 2, 3, 4, 5 \}, \) \( \{1, 2 \}, \{ 1, 2, 3 \}, \{ 1, 2, 4 \}, \{ 1, 2, 5 \}, \{ 1, 2, 3, 4 \}, \{ 1, 2, 4, 5 \}, \{ 1, 2, 3, 5 \}, \{ 1, 2, 3, 4, 5 \} \} \) [ 3 marks ]
\( \{ x : x > 4 \wedge x < 8 \} \)
\( \{ (x, y) : x < 4 \wedge x >= y \} \)
\( \{ x \cup y: x \subseteq F \wedge y \subseteq \{1, 2\} \} \)
Graph Theory [ 7 marks ]
Look at the following graph (you may move the nodes by clicking and dragging to see it more clearly):
- Answer the following two questions: Is this graph directed? Is this graph connected? [ 1 marks ]
Directed: no. Connected: yes.
- Draw an adjacency matrix for this graph. [ 2 marks ]
| | n0 | n1 | n2 | n3 | n4 | n5 | n6 | |--|----|----|----|----|----|----|----| |n0| 2 | 0 | 0 | 0 | 2 | 2 | 2 | |n1| 0 | 0 | 0 | 0 | 1 | 0 | 0 | |n2| 0 | 0 | 0 | 0 | 1 | 0 | 0 | |n3| 0 | 0 | 0 | 0 | 0 | 0 | 1 | |n4| 2 | 1 | 1 | 0 | 0 | 0 | 0 | |n5| 2 | 0 | 0 | 0 | 0 | 0 | 0 | |n6| 2 | 0 | 0 | 1 | 0 | 0 | 2 | - Using set notation, write out all nodes of this graph that are not part of any cycle [ 1 mark ]
\( \{n3, n1, n2 \} \)
- Using set notation write out all the nodes of this graph with loops. [ 1 mark ]
\( \{ n0, n6 \} \)
- What is the degree of node
n0? [ 1 mark ]8
- What is the minimum degree of this graph? [ 1 mark ]
1
Part 3: Statistics [ 40 marks ]
Calculating Statistics [ 13 marks ]
-
Implement the following methods in Java. [ 8 marks ]
/** * Identify if someone's IQ is statistically sigificantly above the mean for the * population, using the values provided to the function. * @param iq - individual's IQ * @param mean - population mean * @param sd - population standard deviation * @return true if iq significantly above the mean **/ static boolean hasAboveAverageIQ(double iq, double mean, double sd) /** * Identify if the average IQ of a group is statistically significantly different * to the mean of the population, using the values provided to the function. * @param group - array of iq scores of group * @param mean - population mean * @param sd - population standard deviation * @return true if mean iq of group is significant **/ static boolean hasSignificantIQGroup(double[] group, double mean, double sd) /** * Perform a two-sample t-test (not assuming equal variance between groups) * @param group1 - array of scores * @param group2 - array of scores * @param expectedMeanDifference - expected difference between group means * @return t statistic **/ static double twoSampleTTest(double[] group1, double[] group2, double expectedMeanDifference) /** * Finds the product-moment correlation co-efficient for two arrays of correlated data * @param x - x values * @param y - y values * @return the calculated pearson's r **/ static double pearsonsR(double[] x, double[] y)
Running Average
It’s often necessary to calculate statistics on a live stream of data without storing all of it due to storage and processing limitations. For example, imagine calculating the mean temperature of a sensor. If the mean was calculated from an array of such readings, this array would in time get unmanigably large.
- Implement the following methods in Java. [ 2 marks ]
/**
* Updates a running mean.
* @param currentMean - The mean found by averaging the first `n` numbers of a stream
* @param newNumber - The next number to include in the mean
* @param n - the number of numbers averaged so far in the mean
* @return the updated mean
**/
static double updateMean(double currentMean, double newNumber, int n)
Neural Networks
Neural networks are used for machine learning and machine learning is really a fancy word for computers doing lots of statistics. Neural networks are composed of neurons. Each neuron in a neural network only does simple computation. These neurons are connected together, so the output of one neuron is the input to another. These connections form a network, hence: ‘neural network’.
Here we’re going to write the code for a single neuron. A neuron does three things:
- Finds the weighted average of it’s input vector (i.e. its array of inputs), using a vector (i.e. array) of weights.
- Add a bias.
- Pass the result of this into a (sigmoid) activation function.
Following this process calculates a number. This number is called the neuron’s activation, and it is this that would be used as the input to other neurons in the network.
Expressing this mathematically, a neuron takes input vector \( w \), weight vector \( x \) and a bias \( b \) and calculates:
\( \sigma(b + \sum_j w_j x_j) \)
Where \( \sigma \) refers to the sigmoid function:
\[ \sigma(z) = \frac{1}{1 + e^{-z}} \]
- Implement the following methods in Java. [ 3 marks ]
/**
* Calculate the weighted average for an input vector with a vector of weights.
* @param inputVector - Array of numbers to average
* @param weights - Weights associated with each value in the input vector
* @return weighted average plus bias
**/
static double weightedAverage(double[] inputVector, double[] weights)
/**
* Implements the sigmoid activation function described above.
* @param z - input to the sigmoid function
* @return output of the sigmoid function
**/
static double sigmoid(double z)
/**
* Returns the activation of a neuron with the given input vector, weights, and bias
* @param inputVector - Array of numbers to average
* @param weights - Weights associated with each value in the input vector
* @param bias - Bias factor for neuron
* @return the activation of the neuron
**/
static double neuronActivation(double[] inputVector, double[] weights, double bias)
Hypothesis Test [ 13 marks ]
A free-to-play mobile game development company runs an experiment. They have developed two levels, A and B, for their game and want to see which one players spend longest playing.
A between-groups design is used for the experiment. 32 players are randomly assigned to two groups who will be exposed to the new level. Group 1 (16 players) plays level A. Group 2 (16 players) play level B. Using game telemetry the company recorded how long players spent playing each level. It also recorded how many days since the player installed the game.
You will need to analyse the data to see if there is a significant difference in the mean time spent playing each level against an alpha of 0.05.
The full data is available here
Report the following:
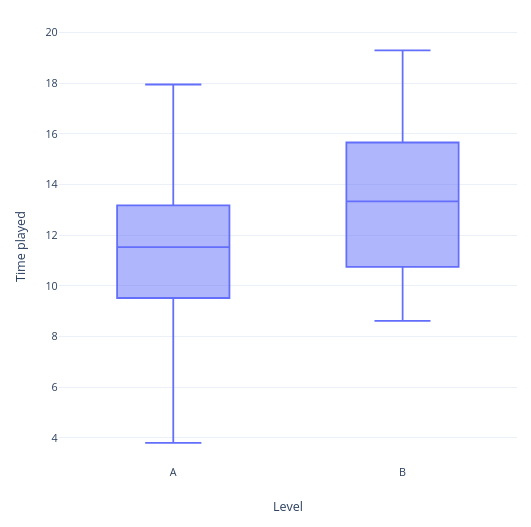
- Mean and standard deviation of play time for each group (2 d.p.) [ 1 mark ]
\( \overline{a} = 11.369531915816221\)
\( \overline{b} = 13.302848351902641\)
\( s_a = 3.45354928809603 \)
\( s_b = 3.17713663523952 \)
Calculate the following by hand, showing your working. You may use a calculator to check your answer, but you must show working to get the mark. If you make use of a table, such as this one to find a value, indicate which table you used in your working. Report your answers to 2 decimal places.
- Appropriate statistical test to use, including formula [ 1 mark ]
- Test statistic [ 1 mark ]
- Degrees of freedom [ 1 mark ]
- P value [ 1 mark ]
- Whether or not result is significant [ 1 mark ]
- An appropriate measure of effect size [ 2 marks ]
Two sample T test
\( t = \frac{(\overline{x}_1 - \overline{x}_2) - 0 }{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} \)
\( t = \frac{(11.369531915816221 - 13.302848351902641) - 0 }{\sqrt{\frac{3.45354928809603^2}{16} + \frac{3.17713663523952^2}{16}}} \)
\( t = \frac{-1.93331643608643}{\sqrt{0.7454376678317872 + 0.6308873249363187}} \)
\( t = \frac{-1.93331643608643}{1.1731687827282593} \)
\( t = -1.6479439826129803 \)
\( df = 32 - 2 = 30 \)
Using 2 tailed t table; \( df = 30 \) , \(t = -1.647943982612967 \)
\( p = 0.1 \) would be \( 1.697 \)
But as \( 1.647 < 1.697 \)
\( p > 0.1 \)
Not significant
\( d = \frac{ \overline{X}_2 - \overline{X}_1 }{ SD_{pooled} } \)
As equal sized groups \( SD_{pooled} = \sqrt{ \frac{ SD_1^{2} + SD_2^{2} }{2}} \)
\( SD_{pooled} = \sqrt{ \frac{3.45354928809603^2 + 3.17713663523952^2}{2}} \)
\( SD_{pooled} = \sqrt{ \frac{11.927002685308596 + 10.0941971989811}{2}} \)
\( SD_{pooled} = \sqrt{11.010599942144847} \)
\( d = \frac{1.93331643608643}{3.3182224069740784} \)
\( d = 0.5826361825606021 \)
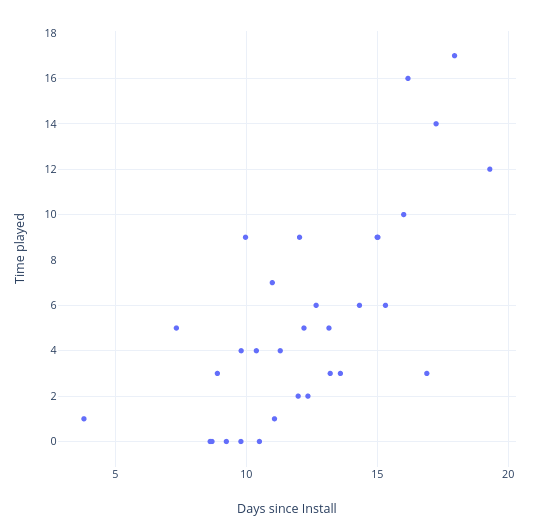
The company wants to see if there is a correlation between skill level and time played across the whole data set (not separated for level). They decide to use time since install as a proxy measure for skill (as players who have had the game a long time are more likely to be skilled in it)
- Perform a linear regression of
days_since_installandtime_played_minutesand find the gradient and intercept of the line of best fit. Give answers to 2 decimal places. Show your working. [ 2 marks ]
\( b = \frac{\sum{(x_i - \overline{x})(y_i - \overline{y})}}{\sum{(x_i - \overline{x})^2}} \)
\( a = \overline{y} - b\overline{x} \)
\( b = 0.51279 \) (gradient)
\( a = 9.53188 \) (intercept)
Produce the following graphs (You may wish to use https://plotly.com/chart-studio/ as we did during the practical):
- Visualise this hypothesis test using a box-plot [ 1 mark ]
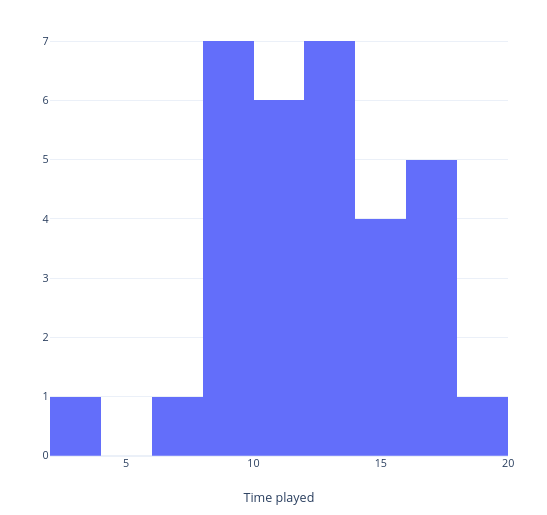
- Visualise the distribution of time played for all players with a histogram [ 1 mark ]
- Visualise the correlation between enjoyment and time played using an appropriate graph [ 1 mark ]
Probability [ 16 marks ]
I have a bag with 12 balls of different colours: 4 red, 4 green, 4 blue. Of each colour there are 2 small balls.
- In an experiment, I draw a ball at random out of the bag. Illustrate this experiment with a Venn diagram, showing the number of outcomes for each combination of events. [ 1 mark ]
- I draw two balls and then replace them. What is the probability that I drew a small red ball and a small green ball? [ 1 mark ]
\(P(1st draw) = \frac{2}{12} \)
\(P(2nd draw) = \frac{2}{11} \)
\(P((1st draw \cap 2nd draw) = \frac{2}{12} \times \frac{2}{11} = \frac{4}{132} = \frac{1}{33} \)
- I draw three balls, one after the other (and later replace them). Considering the colours of the balls, how many permutations might I draw? [ 1 mark ]
\( 3 \times 3 \times 3 = 27 \)
- What is the probability of drawing three balls of the same colour? [ 1 mark ]
\( P(red_1 \cap red_2 \cap red_3) = \frac{4}{12} \times \frac{3}{11} \times \frac{2}{10} \)
\( = \frac{24}{1320} = \frac{1}{55} \)
As this is the same for green and blue, and these probabilities are independent, we can add them:
\( \frac{1}{55} + \frac{1}{55} + \frac{1}{55} = \frac{3}{55} = \frac{72}{1320} \)
\( = 0.054 \)
I remove 3 balls and make a black dot on them.
- What is the probability of drawing either a red ball or a ball with a dot on it? [ 1 mark ]
\( P(red) = \frac{4}{12} \)
\( P(dot) = \frac{3}{12} \)
\( P(red \cup dot) = \frac{4}{12} + \frac{3}{12} - (\frac{4}{12} \times \frac{3}{12} ) \)
\( = \frac{7}{12} - \frac{1}{12} = \frac{1}{2} \)
I purchase two more bags, so now I have three. These have the following numbers of balls in them:
bag 2: 6 red, 2 green, 1 blue
bag 3: 5 green, 5 blue
- I pick one of three bags at random, what is the liklihood that I draw a red ball? [ 2 mark ]
For this we use the Law of Total Probability:
\( P(A) = \sum_{i}P(A \cap B_i) = \sum_{i} P(A | B_i) \times P (B_i) \)
\( P(B) = \frac{1}{3} \)
\( P(A | B_1) = \frac{4}{12} \)
\( P(A | B_2) = \frac{6}{9} \)
\( P(A | B_3) = 0 \)
\( P(A) = (\frac{4}{12} \times \frac{1}{3}) + (\frac{6}{9} \times \frac{1}{3}) = \frac{4}{36} + \frac{6}{27} = \frac{36}{108} = \frac{1}{3} \)
The manufacturer of the balls announces that 10% of balls have a defect. If you drop a ball, there is normally a 20% chance it will break, but this probability rises to 50% if the ball is defective.
- I drop a ball to see whether it breaks. Illustrate all the possible outcomes of the experiment using a Probability Tree. [ 1 mark ]
- I drop a ball and it doesn't break. What is the probability it is not defective? [ 2 mark ]
- I want to be 95% sure the balls I have are not defective. How many times do I need to drop each ball to be this confident? [ 3 marks ]
- I pick a ball at random and drop it twice. What is the chance it will break? [ 1 mark ]
- Implement the following method in Java. [ 2 marks ]
\( P(A|B) = \frac{ P(B|A) \times P(A) }{P(B)} \)
\( P(B) = \sum_{i} P(B | C_i) \times P (C_i) \)
\( P(B|C_{norm}) \times P(C_{norm}) = 0.8 \times 0.9 = 0.72\)
\( P(B|C_{def}) \times P(C_{def}) = 0.5 \times 0.1 = 0.05 \)
\( P(B) = 0.72 + 0.05 = 0.77 \)
\( \frac{P(B|C_{norm}) \times P(C_{norm})}{P(B)} = \frac{72}{77} = 0.935064935064935 \)
Prior probability after 1 drop: \( P(H1) = 0.935064935064935 \)
\( P(B|C_{norm}) \times P(C_{norm}) = 0.8 \times \frac{72}{77} = \frac{288}{385} = 0.7480519480519481 \)
\( P(B|C_{def}) \times P(C_{def}) = 0.5 \times \frac{5}{77} = \frac{5}{154} = 0.032467532467532464 \)
\( P(B) = \frac{288}{385} + \frac{5}{154} = 0.7805194805194805 \)
\( \frac{P(B|C_{norm}) \times P(C_{norm})}{P(B)} = \frac{0.7480519480519481}{0.7805194805194805} = 0.9584026622296173 \)
posterior probability after 2 drops: \( P(H2) = 0.9584026622296173 > 95\% \)
\( P(1) = (0.9 \times 0.2) + (0.1 \times 0.5) = \frac{9}{50} + \frac{1}{20} = \frac{23}{100} \)
\( P(2) = \frac{23}{100} + \frac{23}{100} - (\frac{23}{100} \times \frac{23}{100}) \)
\( P(2) = \frac{46}{100} - \frac{529}{10000} \)
\( P(2) = \frac{4071}{10000} -= 0.4071 \)
/**
* Calculates the probability that a random ball will break if dropped a given number of times,
* using the probabilities from the question above.
* @param n - number of times ball is dropped
* @return probability ball will be broken after n drops.
**/
static double simulateNDrops(int n)
This is the end of the assessment.